Binomial Distribution

1. Properties

Situation: n sequential Bernoulli experiments, with success rate p for a single trial. Single trials are independent from each other.

A binomial experiment (also known as a Bernoulli trial) is a statistical experiment that has the following properties:

1. The experiment consists of n repeated trials.
2. Each trial can result in just two possible outcomes. We call one of these outcomes a success and the other, a failure.
3. The probability of success, denoted by P, is the same on every trial.
4. The trials are independent; that is, the outcome on one trial does not affect the outcome on other trials.

2. Theory

We are only interested in the number of successes in total after n trials, random variable X is then:

X = “ Number of successes in n trials”

This leads to a sample space of

Ω = {0, 1, 2, . . . , n}

What is the general expression for pX(k) for all possible k = 0, . . . , n

pX(k) = P(X = k)

We want to find the probability, that in a sequence of n trials there are exactly k successes.

Now, there are possible ways of selecting k numbers out of the n possible numbers.

So, if s is a sequence with k successes and n−k failures, we already know the probability:

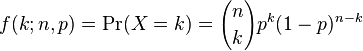
This probability mass function is called the Binomial mass function.