Common Terms to know

1. Discrete probability distribution

If a random variable is a discrete variable,ie, if it can only take on a finite number of values, its probability distribution is called a discrete probability distribution.

For example, flipping a coin and count the number of heads.

X is called a discrete random variable, if

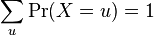
as u runs through the set of all possible values of X.

2. Probability mass function

In probability theory and statistics, a probability mass function (pmf) is a function that gives the probability that a discrete random variable is exactly equal to some value.

The probability mass function is often the primary means of defining a discrete probability distribution, and such functions exist for either scalar or multivariate random variables whose domain is discrete.

A probability mass function differs from a probability density function (pdf) in that the latter is associated with continuous rather than discrete random variables.